| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
| 29 | 30 |
- 코어 자바스크립트
- 리트코드
- 타임어택
- 손에 익히며 배우는 네트워크 첫걸음
- HTTP
- 백준
- 제로초
- 프로그래머스
- 파이썬
- codestates
- 2주 프로젝트
- 리덕스
- 정재남
- programmers
- 자바스크립트
- 회고
- 리액트
- javascript
- 코드스테이츠
- til
- js
- LeetCode
- 토익
- 알고리즘
- 4주 프로젝트
- 타입스크립트
- SQL 고득점 Kit
- python
- 렛츠기릿 자바스크립트
- 타입스크립트 올인원
- Today
- Total
Jerry
알고리즘 / 자료구조 모의면접 질문 리스트 본문
자료구조
자료구조는 데이터의 표현 및 저장 방법을 의미한다.
알고리즘은 그 저장된 데이터를 처리하는 과정이다.
즉, 자료구조를 알아야 알고리즘은 배울 수 있다.
Stack
스택 자료구조는 말 그대로 데이터를 쌓아 올린다는 의미이다. 문제의 종류에 따라 배열보다 스택에 데이터를 저장하는 것이 더 적합한 방법일 수 있다. 스택은 LIFO(Last-In-First-Out)에 따라 자료를 배열한다. ex) 쌓인 접시
스택의 연산
- pop(): 스택에서 가장 위에 있는 항목 제거
- push(item): item 하나를 가장 윗부분에 추가
- peek(): 스택의 가장 위에 있는 항목 반환
- isEmpty(): 스택이 비어 있을 때 true 반환
스택은 같은 방향에서 아이템을 추가하고 삭제한다는 조건하에 연결 리스트로 구현할 수 있다.
스택이 유용한 경우는 재귀 알고리즘을 사용할 때다. 재귀적으로 함수를 호출해야 하는 경우에 임시 데이터를 스택에 넣어 주고, 재귀 함수를 빠져나와 퇴각 검색(backtrack)을 할 때는 스택에 넣어 두었던 임시 데이터를 빼 줘야 한다. 스택은 이런 일련의 행위를 직관적으로 가능하게 해 준다.
class Stack {
constructor() {
this.array = [];
}
push(item) {
return this.array.push(item);
}
pop() {
return this.array.pop();
}
peek() {
return this.array[this.array.length - 1];
}
empty() {
if (this.array.length == 0) {
return true;
}
return false;
}
}
const stack = new Stack();
stack.push(1);
stack.push(2);
stack.pop(); // 2
console.log(stack.empty());
Queue
큐는 FIFO(First-In-First-Out) 순서를 따른다. ex) 매표소
큐의 연산
- add(item): item을 리스트의 끝부분에 추가
- remove(): 리스트 첫 항목 제거
- peek(): 큐에서 가장 위에 있는 항목 반환
- isEmpty(): 큐가 비어 있을 때 true 반환
큐 또한 연결 리스트로 구현할 수 있다. 연결 리스트의 반대 방향에서 항목을 추가하거나 제거하도록 구현한다면 근본적으로 큐와 같다.
큐에서 처음과 마지막 노드를 갱신할 때 실수가 나오기 쉽다. 코딩할 때 반드시 이 부분을 확인해야 한다.
큐는 너비 우선 탐색을 하거나 캐시를 구현하는 경우에 종종 사용된다.
class Queue {
constructor() {
this.array = [];
}
enqueue(data) {
this.array.push(data);
}
dequeue() {
return this.array.shift();
}
toString() {
let str = "";
for (let i = 0; i < this.array.length; i++) {
str = str + this.array[i] + "\n";
}
return str;
}
head() {
return this.array[0];
}
tail() {
return this.array[this.array.length - 1];
}
empty() {
if (this.array.length == 0) {
return true;
}
return false;
}
}
const queue = new Queue();
queue.enqueue(1);
queue.enqueue(2);
queue.enqueue(3);
queue.dequeue();
console.log(queue.toString());
queue.head();
queue.tail();
queue.dequeue();
queue.dequeue();
console.log(queue.empty());
출처 : 도서 OOOO
Linked List
연결 리스트는 여러 개의 노드로 이루어져 있다.
각각의 노드는 데이터와 다음 노드의 주소를 가지고 있다.
연결 리스트는 새로운 데이터를 추가하거나, 데이터의 위치를 찾거나, 제거하는 기능이 있어야 한다.
1->2->3->4->5라는 연결 리스트는 1, 2, 3, 4, 5는 데이터, ->는 주소이다.이것은 배열로 구현되어 있다. [1, 2, 3, 4, 5]에서 1, 2, 3, 4, 5는 데이터, array[0], array[1] ... 는 데이터 위치를, push 메서드로 데이터 추가, splice 메서드로 데이터 제거할 수 있다.
하지만, 여기선 객체를 통해 배열을 직접 만드는 과정을 알아보겠다.
연결 리스트와 노드를 만든다.
연결 리스트에는 length와 head가 있다.
length는 노드의 개수, head는 첫 노드의 주소를 가리킨다.
let LinkedList = (function () {
function LinkedList() {
this.length = 0;
this.head = null;
}
function Node(data) {
this.data = data;
this.next = null;
}
return LinkedList;
})();
데이터 추가, 검색, 삭제하는 메서드를 구현해보자.
let LinkedList = (function () {
function LinkedList() {
this.length = 0;
this.head = null;
}
function Node(data) {
this.data = data;
this.next = null;
}
LinkedList.prototype.add = function (value) {
let node = new Node(value);
let current = this.head;
if (!current) {
this.head = node;
this.length++;
return node;
} else {
while (current.next) {
current = current.next;
}
current.next = node;
this.length++;
return node;
}
};
// 추가를 굳이 마지막 말고 중간이나 맨 처음에 끼워넣어도 된다.
LinkedList.prototype.search = function (position) {
let current = this.head;
let count = 0;
while (count < position) {
current = current.next;
count++;
}
return current.data;
};
LinkedList.prototype.remove = function (position) {
let current = this.head;
let before,
remove,
count = 0;
if (position === 0) {
remove = this.head;
this.head = this.head.next;
this.length--;
return remove;
} else {
while (count < position) {
before = current;
count++;
current = current.next;
}
remove = current;
before.next = remove.next;
this.length--;
return remove;
}
};
return LinkedList;
})();
let list = new LinkedList();
list.add(1);
list.add(2);
list.add(3);
list.length;
list.search(0);
list.search(2);
list.remove(1);
list.length;
현재 연결 리스트는 한쪽 방향으로만 이동한다. 그래서 뒤로 가기는 불편하다.
이 문제를 해결한 리스트가 이중 연결 리스트로, next에 this.prev를 넣어 각 노드의 이전 노드를 가리키게 하는 방법이다.
this.next가 다음 노드를 가리키듯이 말이다.
뿐만 아니라,
한 노드에서 여러 노드를 연결하는 다중 연결 리스트라는 것도 있다.
this.next를 노드들의 배열로 만들어 사용한다고 한다.
출처 : 제로초(연결 리스트) | https://bit.ly/2SmWUvm
Hash Table
해시 테이블은 어떤 특정 값을 받아, 해당 값을 해시 함수에 통과시켜 index에 저장하는 자료구조다.
보통 배열로 구현한다는데 해시 테이블에 대해서 알아보자.
직접 주소 테이블(Direct Address Table)
DAT라고 줄여 부르겠다.
해시 테이블의 아이디어는 DAT라는 자료구조에서 출발한다.
DAT는 입력받은 value가 key가 되는 데이터 맵핑 방식이다.
class DirectAddressTable {
constructor() {
this.table = [];
}
setValue(value = -1) {
this.table[value] = value;
}
getValue(value = -1) {
return this.table[value];
}
getTable() {
return this.table;
}
}
const myTable = new DirectAddressTable();
myTable.setValue(3);
myTable.setValue(19);
myTable.setValue(33);
console.log(myTable.getTable());
이렇게 DAT를 사용할 때, 들어오는 인자 값을 알면 저장된 index도 함께 알 수 있어서
저장된 데이터에 접근해 값을 가져온다. ( 시간 복잡도 O(1) )
이진트리 탐색처럼 값을 찾아보려고 탐색하고, 연결 리스트처럼 값을 삽입하거나 삭제하면 다른 값이 영향을 받지만...
DAT는 내가 보고 싶은 값이 어디 있는지 알 수 있다.
이런 DAT도 공간 효율성이 좋지 않다는 단점이 있다.
저장된 데이터를 제외한 나머지 빈 공간은 값은 없지만 메모리 공간으로 할당되어 있는 상태다.
(만약, 값의 범위 < 값의 개수 => 메모리 낭비) = "적재율이 낮다"
*적재율 : 값의 개수 / 테이블 크기
즉, DAT는 1, 2, 3 같은 연속적인 값을 저장하거나 범위 차이가 크지 않는 데이터일 경우에
적절한 역할을 하게 된다.
이런 DAT의 단점인 공간 효율성을 보완하기 위해 해시 테이블이 등장한다.
해시 테이블은 테이블 인덱스를 사용하지 않고 해시 함수를 사용한다.
해시 함수는 임의의 길이를 가지는 임의의 데이터를 고정된 길이의 데이터로 맵핑하는 함수다.
이 함수에서 나오는 반환 값을 해시라고 한다.
function hashFunction(key) {
return key % 10;
}
console.log(hashFunction(357890987654));
console.log(hashFunction(11));
console.log(hashFunction(4));
위 해시 함수는 무조건 들어온 값을 무조건 0~9 사이의 값을 반환을 보장한다.
DAT와 다르게 큰 수가 들어와도 고정된 테이블 길이를 정해둘 수 있어서 그 안에만 데이터를 저장할 수 있게 된다.
const myTableSize = 5;
const myHashTable = new Array(myTableSize);
function hashFunction(key) {
return key % myTableSize;
}
myHashTable[hashFunction(1991)] = 1991;
myHashTable[hashFunction(5555)] = 55555;
myHashTable[hashFunction(987678987)] = 987678987;
console.log(myHashTable);
키로 들어온 인자들은 해시 테이블 크기보다 훨씬 크지만, 해시 함수를 거치면 일정 범위 값만 반환돼
DAT의 공간 효율성 단점을 보완한다.
해시 함수 특성 중 하나로 해싱만 보고 인자로 어떤 값을 받았는지 추측하기 힘들다.
이러한 특성으로 암호학에서 잘 사용한다.
하지만!!!
눈치챈 사람이 있을 거다. 해시 테이블도 단점이 있다.
해시 충돌이라고 불리는데, 여러 가지 서로 다른 값을 해시 함수에 넣다 보면
같은 값이 나오는 경우가 충돌(collision)이 났다고 한다.
근본적으로 충돌을 완벽히 방지하는 것은 힘들지만,
어느 정도 최소화 혹은 우회하는 방법이 있다.
1. 개방 주소법(Open Address)과 2. 분리 연결법(Separate Chaining) 두 가지가 있다.
개방 주소법은 해시 충돌 발생 시,
테이블 내 새로운 주소를 탐사(Probe) 후, 비어있는 곳에 충돌 데이터를 입력하는 방식이다.
이처럼 다른 인덱스를 허용한다는 의미로 개방 주소라고 한다.
개방 주소법은 (1) 선형 탐색법 (2) 제곱 탐사법 (3) 이중 해싱이 있다.
분리 연결법은 연결 리스트나 트리를 사용한다.
해시 테이블은 고정된 공간을 할당하기 때문에 데이터가 많아질수록
언젠가 데이터가 넘칠 것이다.
그러기 때문에, 데이터를 채우기보다는 크기를 상황에 따라 비우거나 늘려줘야 한다. (Resizing)
출처 : Evans Library | https://bit.ly/3vOq83P
Graph
컴퓨터 공학에서 그래프는 거미줄처럼 여러 개 점들이 선으로 이어져 있는 복잡한 네트워크 망과 같은 모습이다.
정리하면, 여러 개 점들끼리 연결된 복잡한 관계를 표현한 자료구조라고 할 수 있을 것이다.
그래프에서 점은 정점(vertex), 선은 간선(edge)라고 표현합니다.

우리 실생활에서 그래프 자료구조를 알게 모르게 사용하고 있습니다. ex) 포털 사이트의 검색 엔진, SNS, 내비게이션의 길 찾기
서울에 사는 A는 부산에 사는 B와 오랜 친구 사이입니다. 이번 주말에 B의 결혼식이 있다고 하여 A는 차를 몰고 부산으로 가려고 합니다. 마침, 대전에 살고 있는 A와 B의 친구 C도 참석을 한다고 하여 A는 대전에서 C를 태워 부산으로 이동을 하려고 합니다
위 예제를 정점과 간선으로 나타내면,
- 정점: 서울, 대전, 부산
- 간선: 서울-대전, 대전-부산, 부산-서울
으로 나타낼 수 있습니다.
하지만, 정점끼리 연결되어 있지만 각 정점 간의 거리를 알 수 없습니다.
연결된 사실만 알려줄 뿐입니다.
이런 걸, 가중치(연결 강도)가 적혀있지 않다고 하며, 이런 그래프를 비가중치 그래프라고 부릅니다.
let isConnected = {
seoul: {
busan: true,
daejeon: true
},
daejeon: {
seoul: true,
busan: true
},
busan: {
seoul: true,
daejeon: true
}
}
console.log(isConnected.seoul.daejeon) // true
console.log(isConnected.daejeon.busan) // true
그렇다면, 가중치 그래프로 표현하면 아래와 같습니다.
- 정점: 서울, 대전, 부산
- 간선: 서울-140km-대전, 대전-200km-부산, 부산-325km-서울

- 무향 그래프(undirected graph) vs 단방향 그래프(directed): 방향이 있고 없고
- 진입 차수(in-degree) vs 진출 차수(out-degree) : 들어오는 간선 vs 나가는 간선
- 인접(adjacency) : 두 정점 간 간선이 이어져 있다면 서로 인접한 정점이다.
- 자기 루프(self loop): 진출 간선이 곧바로 자신에게 진입하는 경우
- 사이클(cycle): 한 정점에서 다른 정점을 거쳐 다시 해당 정점으로 돌아갈 수 있다면 사이클이 있다고 한다. (서울-> 대전-> 부산-> 서울)
그래프 표현방식으로 인접 행렬과 인접 리스트가 있다.
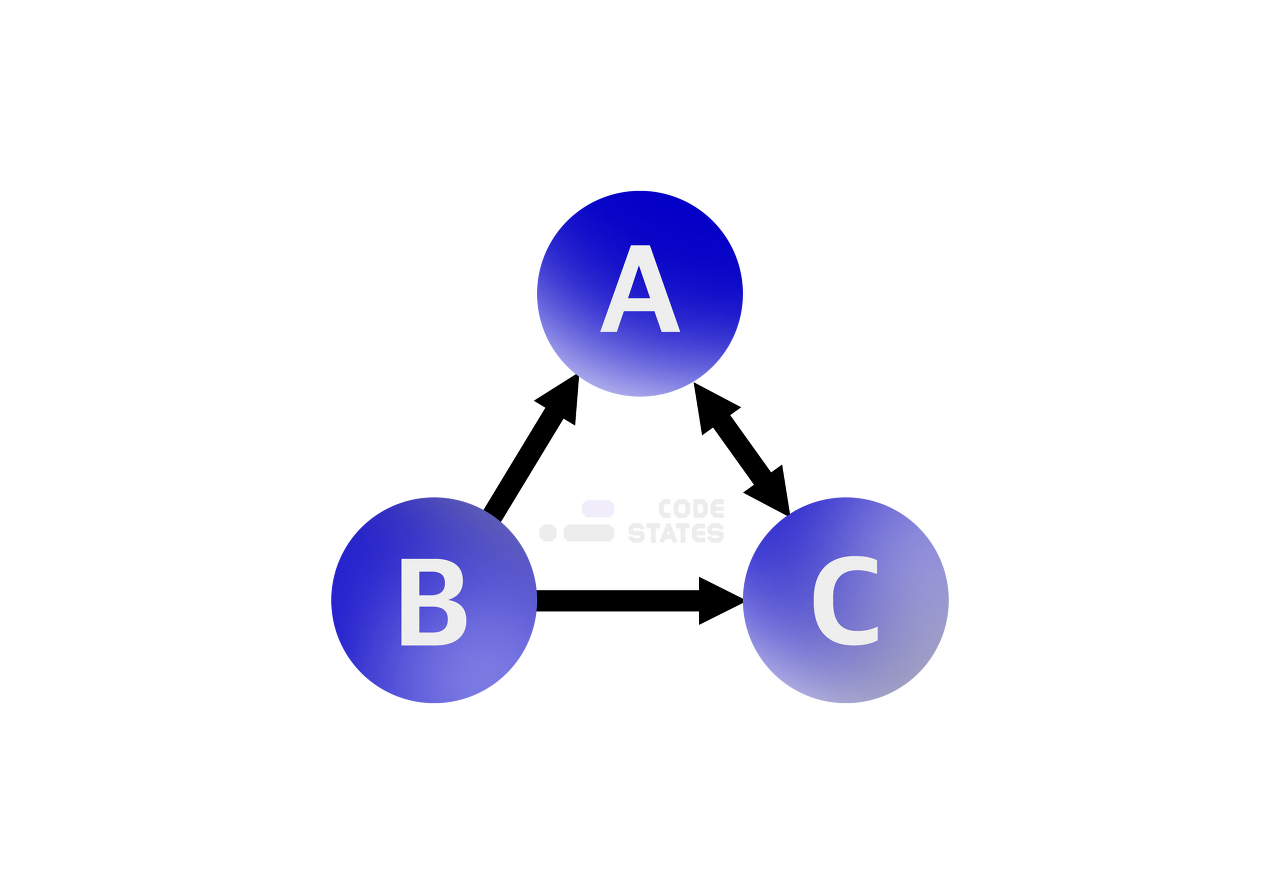
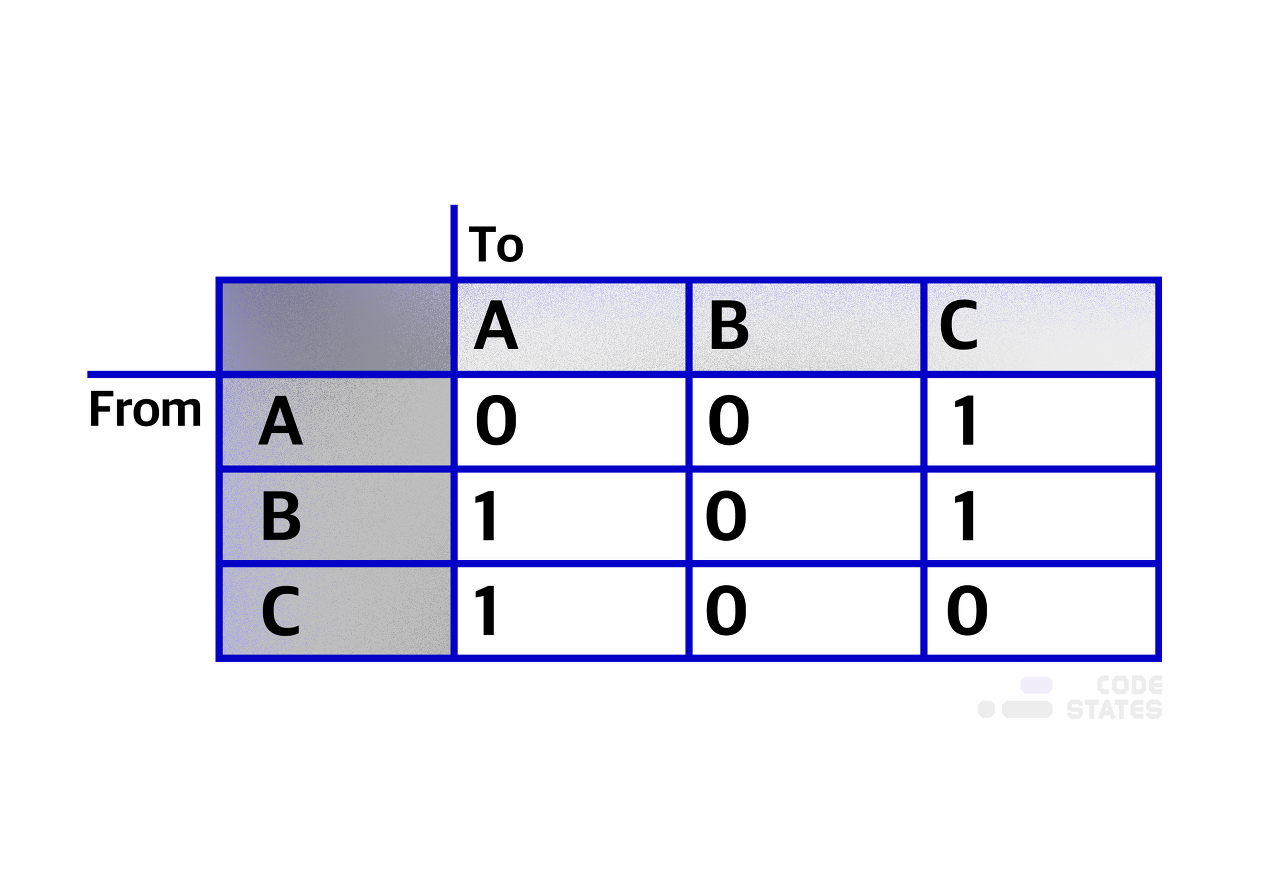
인접 행렬은 정점 간의 인접함을 표시해주는 행렬로 2차원 배열이다.
이어져 있다면 1, 않다면 0으로 표시한다.
인접 행렬은 두 정점 사이의 관계 파악을 할 때, 가장 빠른 경로를 찾을 때 주로 사용됩니다.
인접 리스트는 각 정점이 어떤 정점과 인접한 지 리스트 형태로 볼 수 있습니다.
그렇다는 건, 각 정점마다 리스트를 가지고 있다는 것이며,
리스트 안에는 해당 정점과 인접한 정점 정보가 담겨 있을 겁니다.
ex) A->C->Null, B->A->C->Null, C->A->Null
Q: 예시에서, B는 A와 C로 이어지는 간선이 두 개가 있는데, 왜 A가 C보다 먼저일까? 순서는 중요할까?
A: 중요하지 않다. 자료구조는 구현하는 자의 편의/목적에 따라 기능을 추가/삭제할 수 있기 때문에, 우선순위별 / 단순한 나열로 담을 수 있다.
인접 행렬은 연결 가능한 모든 경우의 수를 저장하지만,
인접하지 않으면 0, 인접하면 1을 저장하기 때문에 메모리를 많이 차지한다.
=> 메모리 효율을 생각하면 인접 리스트를 사용한다.
let Graph = (function () {
function Vertex(key) {
this.next = null;
this.edge = null;
this.key = key;
this.inTree = null;
}
function Edge(data, dest, capacity) {
this.nextEdge = null;
this.destination = dest;
this.data = data;
this.capacity = capacity;
this.inTree = null;
}
function Graph() {
this.count = 0;
this.first = null;
}
Graph.prototype.insertVertex = function (key) {
let vertex = new Vertex(key);
let last = this.first;
if (last) {
while (last.next !== null) {
last = last.next;
}
last.next = vertex;
} else {
this.first = vertex;
}
this.count++;
};
Graph.prototype.deleteVertex = function (key) {
let vertex = this.first;
let prev = null;
while (vertex.key !== key) {
prev = vertex;
vertex = vertex.next;
}
if (!vertex) return false;
if (!vertex.edge) return false;
if (prev) {
prev.next = vertex.next;
} else {
this.first = vertex.next;
}
this.count--;
};
Graph.prototype.insertEdge = function (data, fromKey, toKey, capacity) {
let from = this.first;
let to = this.first;
while (from && from.key !== fromKey) {
from = from.key;
}
while (to && to.key !== toKey) {
to = to.next;
}
if (!from || !to) return false;
let edge = new Edge(data, to, capacity);
let fromLast = from.edge;
if (fromLast) {
while (fromLast.nextEdge !== null) {
fromLast = fromLast.nextEdge;
}
fromLast.nextEdge = edge;
} else {
from.edge = edge;
}
};
Graph.prototype.deleteEdge = function (fromKey, toKey) {
let from = this.first;
while (from !== null) {
if (from.key === fromKey) break;
from = from.next;
}
if (!from) return false;
let fromEdge = from.edge;
let preEdge;
while (fromEdge !== null) {
if (toKey === fromEdge.destination.key) break;
preEdge = fromEdge;
fromEdge = fromEdge.next;
}
if (!fromEdge) return false;
if (preEdge) {
preEdge.nextEdge = fromEdge.nextEdge;
} else {
fromEdge = fromEdge.nextEdge;
}
};
return Graph;
})();
let graph = new Graph();
graph.insertVertex("A");
graph.insertVertex("B");
graph.insertVertex("C");
graph.insertVertex("D");
graph.insertVertex("E");
graph.insertVertex("F");
graph.insertEdge(1, "A", "B");
graph.insertEdge(1, "B", "C");
graph.insertEdge(1, "B", "E");
graph.insertEdge(1, "C", "E");
graph.insertEdge(1, "C", "D");
graph.insertEdge(1, "E", "D");
graph.insertEdge(1, "E", "F");
출처 : Codestate, 제로초(그래프) | https://bit.ly/35IpFFW
Tree
이번에 알아볼 트리 (자료) 구조는 나무를 거꾸로 놓은 듯한 모습입니다.
그래프의 여러 구조 중 일방향 그래프의 한 구조입니다.
트리 구조는 가계도와 비슷합니다.
데이터가 바로 아래에 있는 하나 이상의 데이터에 단방향으로 연결되는 계층적 자료구조입니다.
순차적으로 나열된 선형 구조가 아닌, 여러 개의 데이터가 존재할 수 있는 비선형 구조입니다.
계층적으로 아래로 뻗기 때문에 사이클이 없습니다.
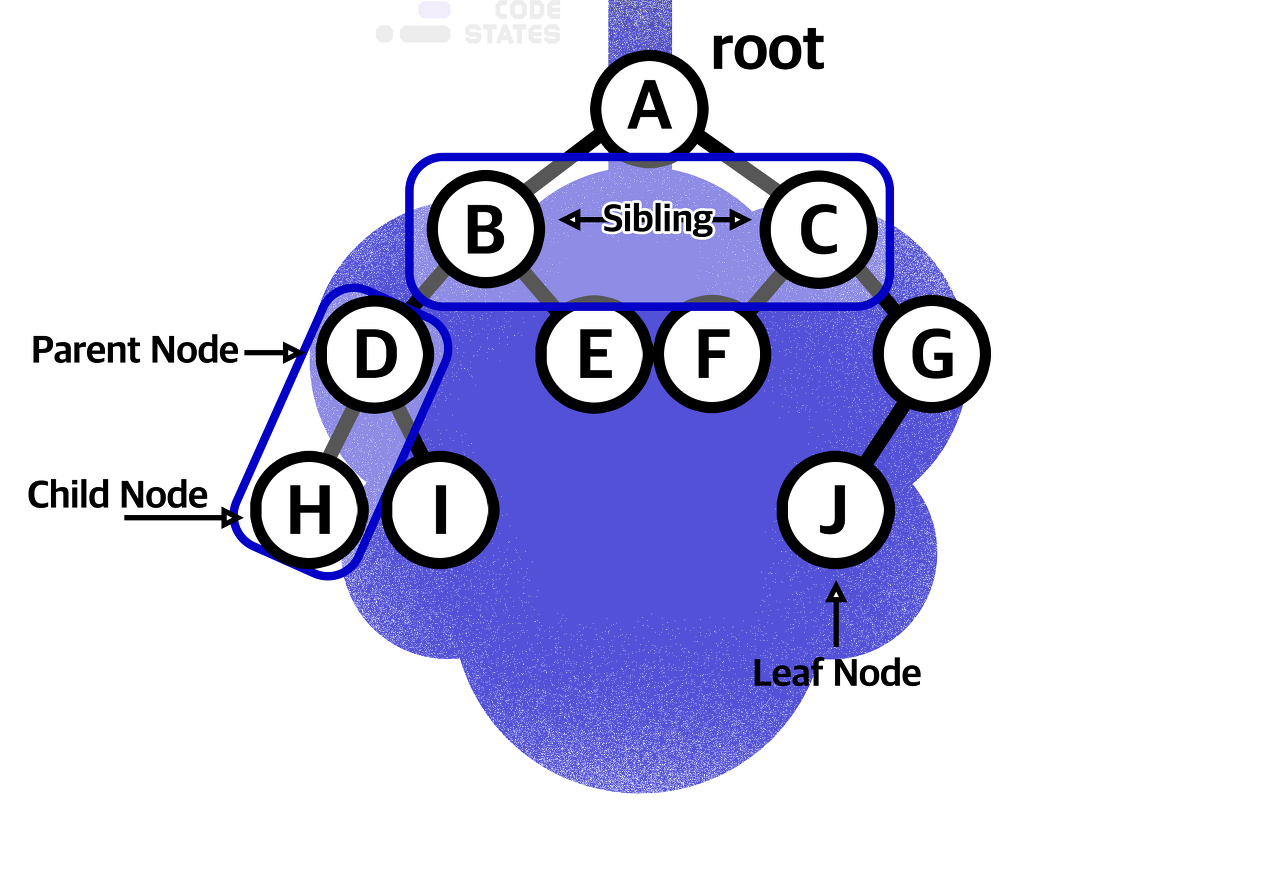
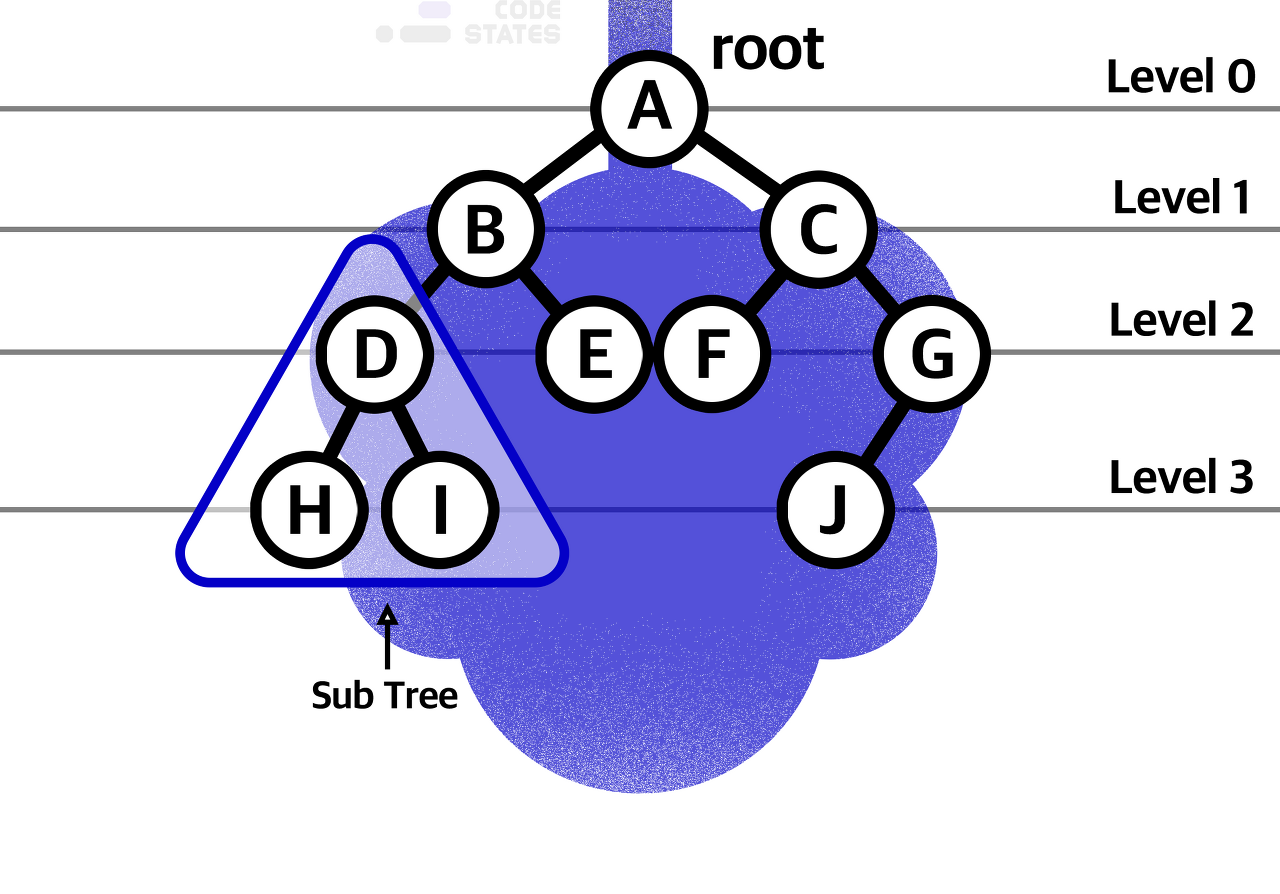
트리 구조는 루트라는 꼭짓점 데이터를 시작으로 여러 개의 데이터를 간선으로 연결합니다.
- 이 데이터를 노드라고 하며, 상위 노드와 하위 노드는 부모/자식 관계를 가집니다.
- 자식이 없는 노드는 리프 노드라고 합니다.
- 루트와 자신과의 거리를 레벨(level)이라고 부르며, 루트가 level 1입니다.
- 루트부터 가장 안쪽 노드까지 레벨(edge 개수)을 높이(height)라고 하며,
- 특정 노드부터 루트까지 레벨을 깊이(depth)라고 합니다.
- 같은 레벨 노드는 형제 노드(sibling node)라고 합니다.
- 트리 아래 트리가 계속 나오기 때문에 재귀 함수가 사용됩니다.
트리 구조는 HTML 구조, 컴퓨터 디렉터리 구조, 월드컵 토너먼트 대진표, 가계도, 조직도 등의 실생활 예시로 사용됩니다.
이렇듯 편리한 구조를 전시에 사용되지만, 효율적인 탐색을 위해 사용합니다.
트리 종류 중 많이 사용하는 이진트리(binary tree)와 이진 탐색 트리(binary search tree)에 대해 알아보겠습니다.
이진트리(binary tree)
자식 노드가 최대 두 개인 노드들로 구성된 트리를 이진트리라고 합니다.
- 자식을 왼쪽 자식과 오른쪽 자식으로 분류합니다.
- 이진트리는 자료의 삽입, 삭제에 따라 정 이진트리(Full binary tree), 완전 이진트리(Complete binary tree), 포화 이진트리(Perfect binary tree)로 나뉩니다.

- 완전 이진트리: 마지막 레벨 제외한 모든 노드가 가득 차있고, 마지막 레벨의 노드는 전부 차있지 않아도 되지만 왼쪽이 채워져야 합니다.
- 정 이진트리: 각 노드가 0개 혹은 2개의 자식 노드를 갖습니다.
- 포화 이진 트리: 정 이진트리면서 완전 이진트리입니다. 모든 리프 노드 레벨 동일, 모든 레벨이 가득 채워있습니다.
이진 탐색 트리(binary search tree)
모든 왼쪽 자식들은 루트나 부모보다 작은 값이고, 모든 오른쪽 자신들은 루트나 부모보다 큰 값인 특징이 있는 이진트리입니다.
- 이진 탐색 트리는 균형 잡힌 트리가 아닐 때, 입력되는 값의 순서에 따라 한쪽으로 노드가 몰리는 이슈가 있습니다.
- 몰리는 이슈를 해결하기 위해, 삽입과 삭제마다 트리 구조 재조정 과정을 거치는 알고리즘을 도입할 수 있습니다.
트리에 데이터를 넣거나 찾을 때, 제거할 때 대부분 재귀를 사용합니다.
추가하거나 찾기 위해 원하는 위치를 찾을 때까지 오른쪽 왼쪽 찾아가며 재귀를 통해 도달합니다.
지우는 게 문제인데, 지운 후에 트리가 이진 검색 트리 조건을 만족하는지 확인해야 합니다.
지울 때, 고려해야 할 세 가지 경우
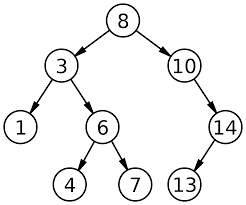
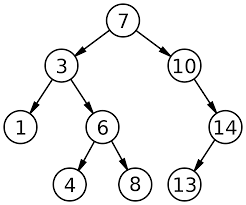
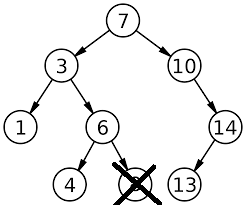
- 왼쪽 자식 노드가 없을 경우(숫자 10 노드)
- 오른쪽 노드를 끌어올려 지워진 공간을 채운다.
- 오른쪽 자식 노드가 없을 경우(숫자 14 노드)
- 왼쪽 노드를 끌어올려 지워진 공간을 채운다.
- 양쪽 자식 노드가 있을 경우(숫자 8 노드)
- 지우고자 하는 8 노드와 8의 왼쪽 자식 중 가징 큰 노드인 7을 교환합니다.
- 7과 8의 자리가 바뀝니다.
- 8은 양쪽 자식이 모두 없으므로, '1. 왼쪽 자식 노드가 없을 경우'처럼 처리합니다.
- 새로운 이진 탐색 트리가 완성됩니다.
let Tree = (function () {
function Tree() {
this.count = 0;
this.root;
}
function Node(data) {
this.data = data;
this.left;
this.right;
}
function _insert(root, node) {
if (!root) return node;
if (node.data < root.data) {
root.left = _insert(root.left, node);
return root;
} else {
root.right = _insert(root.right, node);
return root;
}
return root;
}
Tree.prototype.add = function (data) {
let node = new Node(data);
if (this.count === 0) {
this.root = node;
} else {
_insert(this.root, node);
}
return ++this.count;
};
function _get(data, node) {
if (node) {
if (data < node.data) {
return _get(data, node.left);
} else if (data > node.data) {
return _get(data, node.right);
} else {
return node;
}
} else {
return null;
}
}
Tree.prototype.get = function (data) {
if (this.root) {
return _get(data, this.root);
} else {
return null;
}
};
function _remove(root, data) {
let newRoot, exchange, temp;
if (!root) return false;
if (data < root.data) {
root.left = _remove(root.left, data);
} else if (data > root.data) {
root.right = _remove(root.right, data);
} else {
if (!root.left) {
newRoot = root.right;
return newRoot;
} else if (!root.right) {
newRoot = root.left;
} else {
exchange = root.left;
while (exchange.right) exchange = exchange.right;
temp = root.data;
root.data = exchange.data;
exchange.data = temp;
root.left = _remove(root.left, exchange.data);
}
}
return root;
}
Tree.prototype.remove = function (key) {
let node = _remove(this.root, key);
if (node) {
this.root = node;
this.count--;
if (this.count === 0) this.root = null;
}
return true;
};
return Tree;
})();
let tree = new Tree();
tree.add(5);
tree.add(3);
tree.add(4);
tree.add(2);
tree.add(7);
tree.add(6);
tree.root.left.data;
tree.root.left.left.data;
tree.root.left.right.data;
tree;
tree.remove(3);
tree.root.left.data;
출처 : 코드스테이츠, 제로초 | https://bit.ly/3qeXveS
Heap
힙의 시간 복잡도
- peek() : O(1)
- insert : O(logn)
- remove: O(logn)
- 힙은 주로 최소/최대 값을 O(1)의 시간 복잡도로 얻어내기 위해 사용된다.
- 아래 Mip Heap의 2가지 규칙 덕분에 항상 최상위 노드만 조회하면 최소 값을 얻어낸다.
- 배열이나 연결 리스트 같은 자료구조는 최소/최대 값을 얻어내려면 O(n)이 걸린다.
- 이진 탐색을 이용하면 O(logn)까지 줄일 수 있다.
- Heap 사용처
- Min Heap 특성상 우선순위 큐를 구현하는데 최적의 자료구조가 된다.
- Queue 사용처가 Heap의 사용처가 될 수 있다.
- 운영체제에서 우선순위 기반 일들을 스케쥴링하기 위해서 사용
- 다익스트라 알고리즘(최단 거리 구하기 알고리즘)에서 최소 비용을 기반으로 그래프 탐색 시 사용
- Min Heap 특성상 우선순위 큐를 구현하는데 최적의 자료구조가 된다.
- Heap은 Max Heap과 Min Heap으로 나뉜다.
- Max Heap: 부모 노드는 항상 자식 노드보다 크거나 같아야 한다.
- Min Heap: 부모 노드는 항상 자식 노드보다 작아야 한다.
- 힙은 이진트리로 구현한다.
- 힙은 완전 이진트리 구조를 사용하며, 트리 가장 아래층을 제외하고는 상단 모든 레벨이 완전히 채워져야 한다는 규칙이 있다.
- 이진트리는 각각의 부모 노드는 오로지 두 개의 자식 노드만을 가질 수 있는 트리이다.
- 위 2가지 규칙을 항상 따르는 힙은 Min Heap이다.
- 이진트리 자료구조임에도 불구하고, 배열로 구현할 수 있다.
- 왼쪽 자식 노드 인덱스 : 부모 노드 인덱스 * 2 + 1
- 오른쪽 자식 노드 인덱스 : 부모 노드 인덱스 * 2 + 2
- 부모 노드 인덱스 : (자식 노드 인덱스 - 1) / 2
- 이진트리 자료구조임에도 불구하고, 배열로 구현할 수 있다.
//! 1. Min Heap 기본 골격
class Heap {
constructor() {
this.heap = [];
}
getLeftChildIndex = (parentIndex) => parentIndex * 2 + 1;
getRightChildIndex = (parentIndex) => parentIndex * 2 + 2;
getParentIndex = (childIndex) => Math.floor((childIndex - 1) / 2);
peek = () => this.heap[0];
//! 2. insert
insert = (key, value) => {
const node = { key, value };
this.heap.push(node);
this.heapifyUp(); //? 배열에 가장 끝에 넣고, 다시 min heap 의 형태를 갖추도록 한다.
};
//! 최근에 삽입한 노드가 제 자리를 찾아 갈 수 있도록 아래로 부터 위로 끌어올려야 한다. 이 함수의 이름을 heapifyUp
heapifyUp = () => {
let index = this.heap.length - 1;
const lastInsertedNode = this.heap[index];
while (index > 0) {
const parentIndex = this.getParentIndex(index);
if (this.heap[parentIndex].key > lastInsertedNode.key) {
this.heap[index] = this.heap[parentIndex];
index = parentIndex;
} else break;
}
this.heap[index] = lastInsertedNode;
};
//! 3. remove
remove = () => {
const count = this.heap.length;
const rootNode = this.heap[0];
if (count <= 0) return undefined;
if (count === 1) this.heap = [];
else {
this.heap[0] = this.heap.pop();
this.heapifyDown(); //? 다시 min heap 의 형태를 갖추도록 한다.
}
return rootNode;
};
//! 변경된 루트노드가 제 자리를 찾아가도록 하는 메소드
// 위에서 부터 아래로 끌어 내려야 하기 때문에 함수의 이름을 heapifyDown 이라고 하자.
heapifyDown = () => {
let index = 0;
const count = this.heap.length;
const rootNode = this.heap[index];
while (this.getLeftChildIndex(index) < count) {
const leftChildIndex = this.getLeftChildIndex(index);
const rightChildIndex = this.getRightChildIndex(index);
const smallerChildIndex =
rightChildIndex < count &&
this.heap[rightChildIndex].key < this.heap[leftChildIndex].key
? rightChildIndex
: leftChildIndex;
if (this.heap[smallerChildIndex].key <= rootNode.key) {
this.heap[index] = this.heap[smallerChildIndex];
index = smallerChildIndex;
} else break;
}
this.heap[index] = rootNode;
};
}
Priority Queue
우선순위 큐는 위 MIn Heap을 상속해 3가지 메서드를 구현한다.
- enqueue: Min Heap에 넣기
- dequeue: Min Heap에서 삭제하기;우선순위가 가장 높은 노드 꺼내기
- isEmpty: heap이 비어있는지 체크하기
class PriorityQueue extends Heap {
constructor() {
super();
}
enqueue = (priority, value) => this.insert(priority, value);
dequeue = () => this.remove();
isEmpty = () => this.heap.length <= 0;
}
출처: 춤추는 개발자 | https://bit.ly/3zNguBx
'Interview > 모의 면접 질문 리스트' 카테고리의 다른 글
| 네트워크/HTTP 모의면접 질문 리스트 (0) | 2021.06.21 |
|---|---|
| JavaScript 모의면접 질문 리스트(2) (0) | 2021.06.11 |
| JavaScript 모의면접 질문 리스트 (0) | 2021.06.10 |
| CS fundamentals 질문에 답해보기! (스압 주의!) (0) | 2021.06.08 |



